General information
Credit scorecards are a very popular approach to the quantitative representation of the probability that clients will be prone to demonstrate some defined behavior, like, for instance, loan default, bankruptcy, or payment without delinquency. Clients are described by a set of attributes that are characterized with the specific partial scores that represent the contribution of the attributes to the final score - the higher score the more tendency to demonstrate the target behavior. The partial scores can be learned from the historical data that connect the clients' features with the target behavior and the commonly used technique, in this case, is Logistics regression. The coefficients of the Logistic Regression model can be transformed to partial scores with scaling so that they reflect the impact of the separate attribute on the final decision and lead to the expected Scores ranges.
There are two popular approaches for the scaling of the Logistics Regression coefficients ( - LogReg coefficient for the variable , - LogReg intercept, n - number of the independent variables ):
- Min-max scaling - transform the LogReg coefficients to the partial scores so that the final clients' scores belong to the min-max range
- Odds-based scaling - transform the LogReg coefficients to the partial scores so that the final clients' scores reflect the credit default odds. This method depends on three parameters - target odds, target score and points to double the odds (pdo): example - target score of 600 to mean a 50 (target odds) to 1 odds of the good customer to bad, and an increase of 20 means a doubling odds)
The scaling procedure can be extended with WOE correction - this approach allows to consider the dependencies in the novel labeled data:
Description
Brick Location
Bricks → Machine Learning → Scorecard
Bricks → Analytics → Credit Scoring → Scorecard
Bricks → Use Cases → Credit Scoring → Credit Scoring Model → Scorecard
Brick Parameters
- Scaling
- Min Score
- Max Score
- Target odds and Target Score
- Points to double the odds
The type of final scores representation. There are two strategies are available - Min-Max scaling and Odds scaling
The minimal value of the client score is expected after the Scorecard brick applying to the trained Logistic regression model. It is expected that the worst situation is described with this score
The maximal value of the client score is expected after the Scorecard brick applying to the trained Logistic regression model. It is expected that the best situation is described with this score
Odds-based scaling parameters - "target score" defines the client with "target odds" to 1 odds of the good customer to bad.
Score increasing value when good/bad odds are doubled
- WoE correction
- Target
- Columns
- remove all mentioned columns from dataset and proceed with the rest ones as with predictors
- use the selected columns as predictors and proceed with them
- Remove all except selected
The binary flag for the adjustment of the score based on WoE considering
A binary variable that is used as a target variable in a binary classification problem. The weight of evidence of the separate attributes is calculated with respect to the specified target. The target variable should be present in the input dataset and takes two values - (0, 1).
List of possible columns for selection. It is possible to choose several columns for filtering by clicking on the '+' button in the brick settings and specifying the way of their processing:
The binary flag, which determines the behavior in the context of the selected columns
Notes
- Scorecard requires the binary feature vector. Please be sure that the Scoring Model meets these requirements.
- Scorecards adjustment with Data Sampling requires the consistency between WoE and LogReg coefficient for the correspondent categories, otherwise, these categories will be excluded from the resulted Scorecards.
Example of usage
Let's consider the binary classification problem . The inverse target variable takes two values - survived (0) - good or non-event case / not-survived (1) - bad or event case. The general information about predictors is represented below:
- passengerid (category) - ID of passenger
- name (category) - Passenger's name
- pclass (category) - Ticket class
- sex (category) - Gender
- age (numeric) - Age in years
- sibsp (numeric) - Number of siblings / spouses aboard the Titanic
- parch (category) - Number of parents / children aboard the Titanic
- ticket (category) - Ticket number
- fare (numeric) - Passenger fare
- cabin (category) - Cabin number
- embarked (category) - Port of Embarkation
We need to get the scorecard that allows to assess the Survival Score of the passenger.
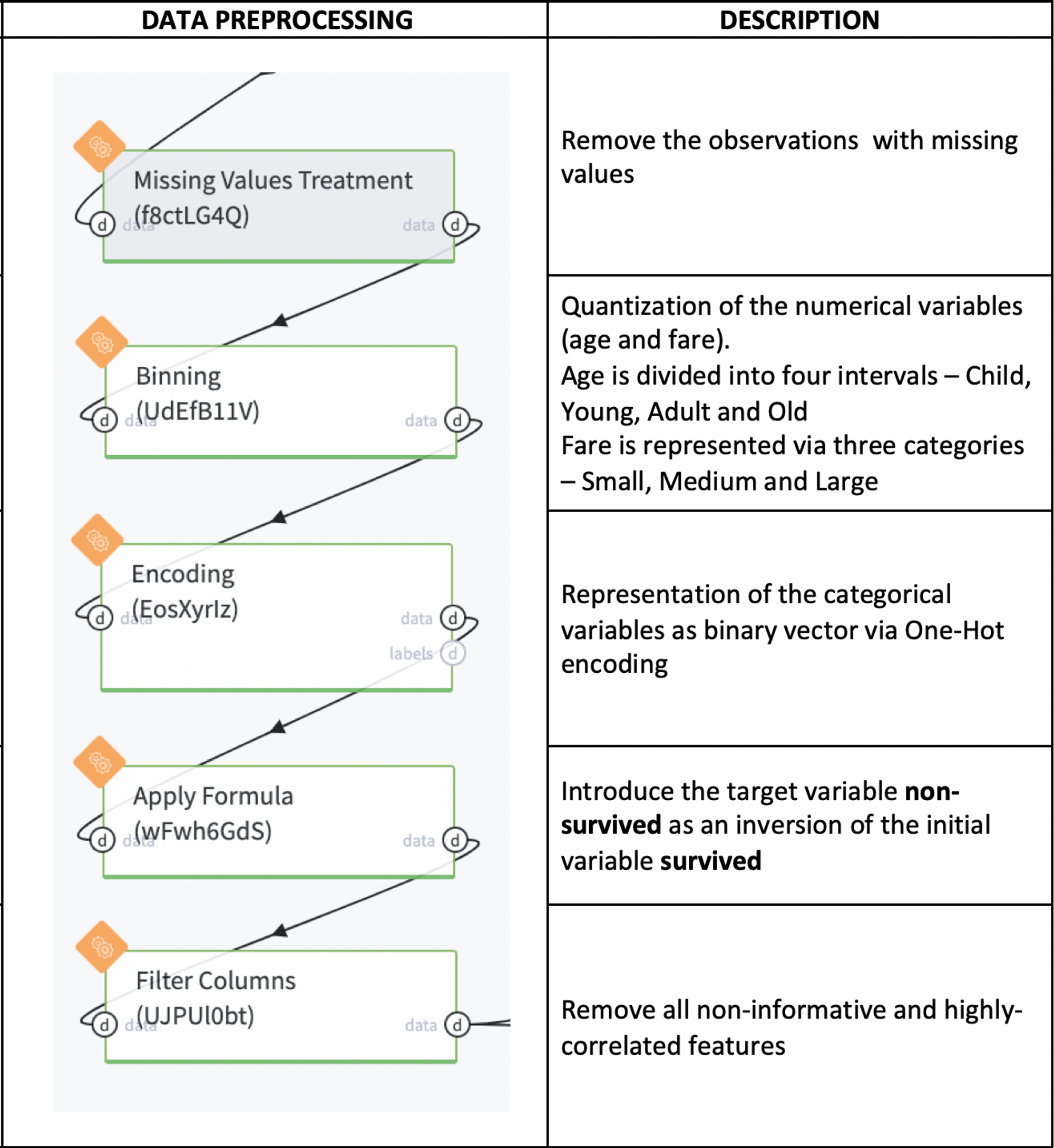
Data Processing Pipeline description
For getting the Scorecard we need to train the Logistics Regression model, which returns the probability of Not-Survive (0 - if the passenger survived and 1 otherwise). The feature-vector of the Logistic regression should be represented in the binary form, that's why we need to make some data preprocessing - encoding of the categorical features and binning with the further encoding of the numerical ones.
The demo pipeline with the Scorecard brick is represented below
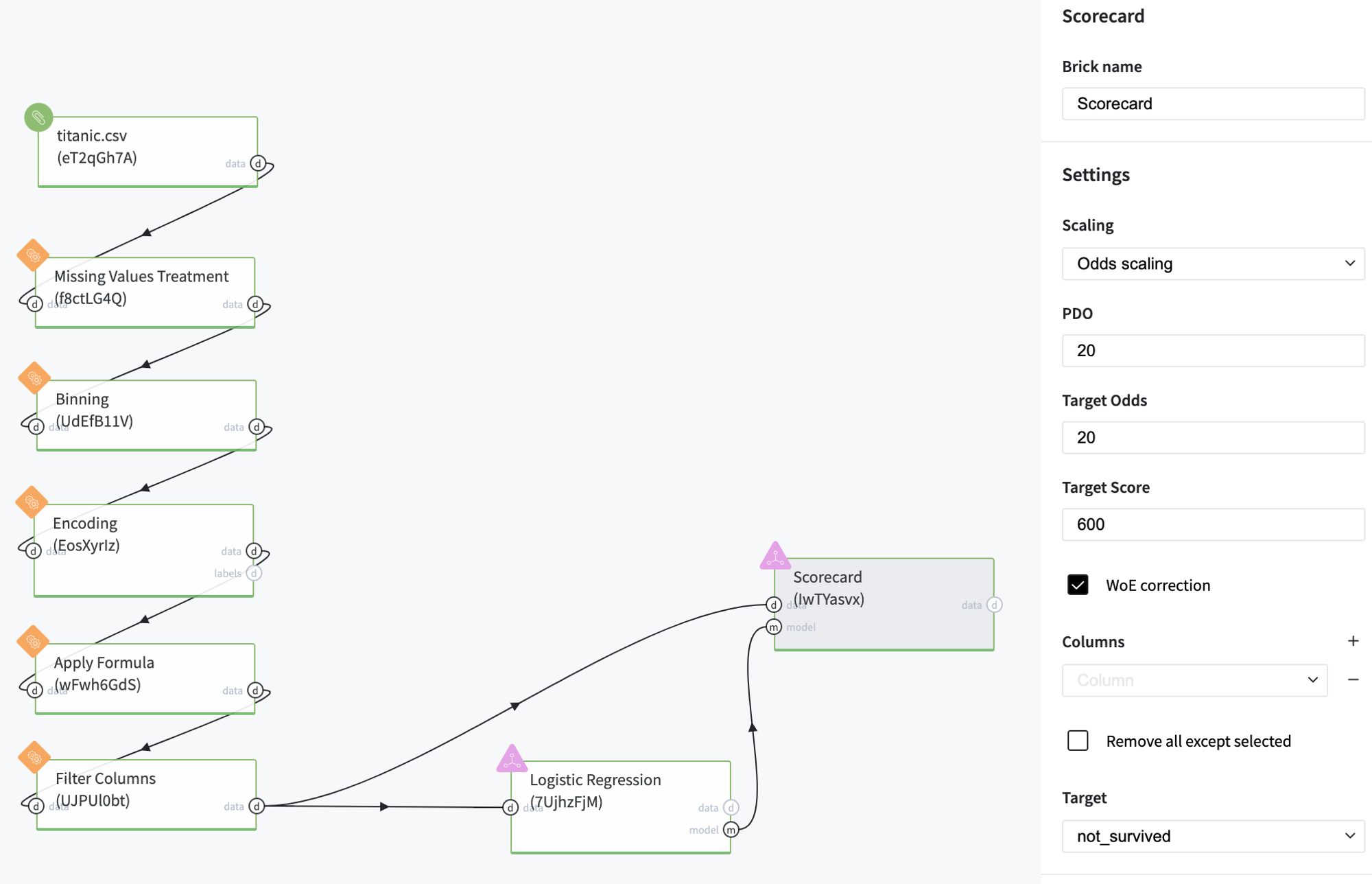
Scorecard brick should be connected with Logistics Regression and can accept the dataset with the corresponded structure for the WoE adjustment. In this case, we used Odds Scaling with the Target score of 600, which corresponds to the Target odds of 20 to 1. The final Scorecard is depicted below:
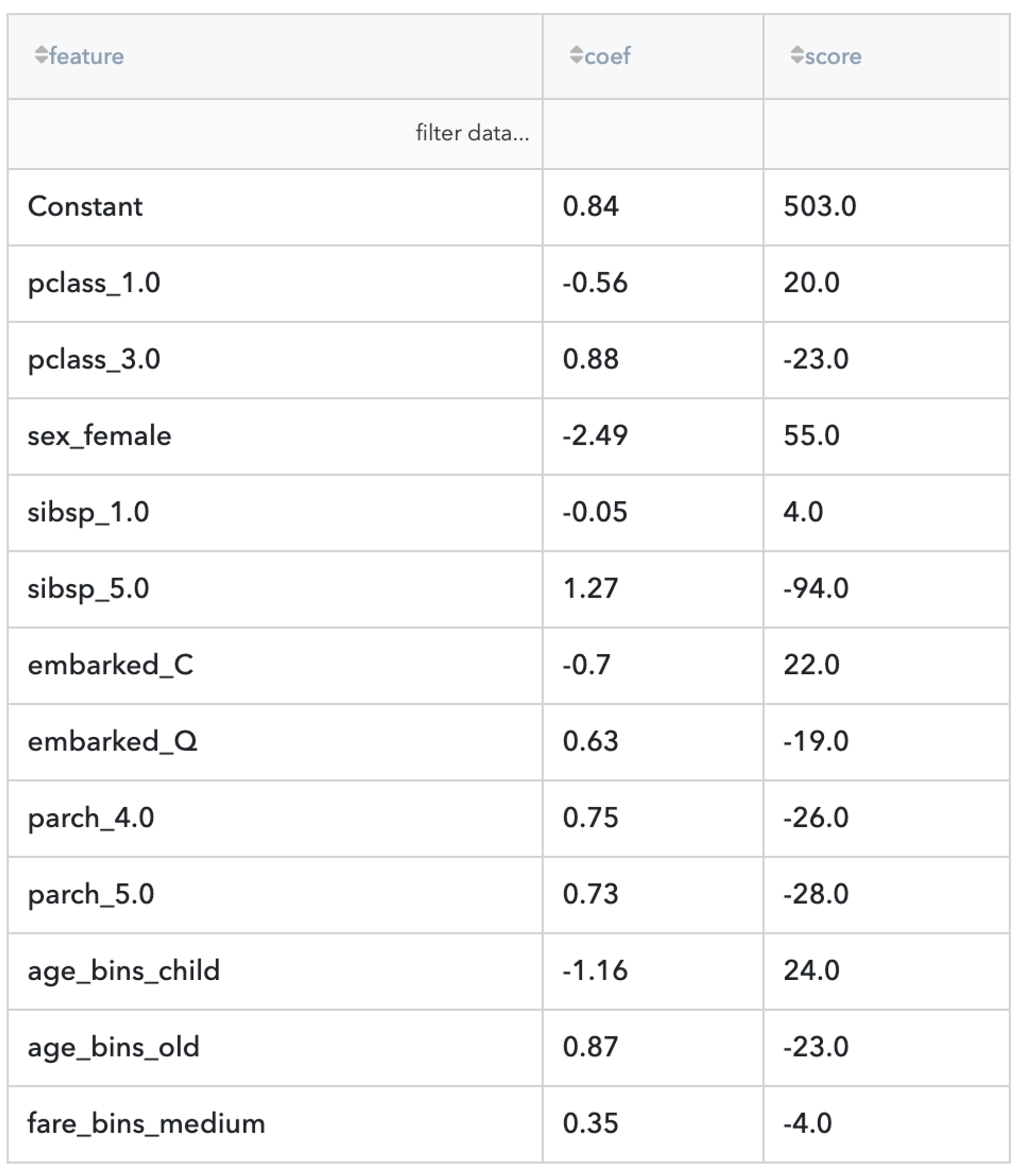
The resulted table has three columns - Feature (scored attribute), Coef(coefficients of the trained Logistic regression model) and Score (partial scores for the attributes). As the model predicts the chance of non-surviving, the partial scores, which contribute to the surviving score, have the opposite sign to the LogReg coefficients.
It's not difficult to see that if the passenger belongs to the female group or is a child or is traveling in the first class - they have more chances for surviving. On the other hand, the "third class" attribute is extremely decreased the Surviving score.